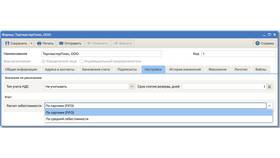
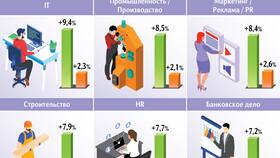
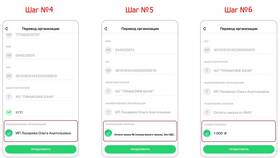
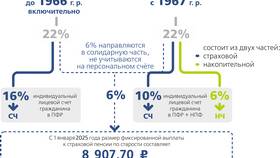
Сумма величин представляет собой результат сложения двух или более числовых значений, физических параметров или математических объектов. Это фундаментальное понятие математики и физики, имеющее широкое применение в различных областях знаний.
Содержание
Сумма величин представляет собой результат сложения двух или более числовых значений, физических параметров или математических объектов. Это фундаментальное понятие математики и физики, имеющее широкое применение в различных областях знаний.
Основное определение
Сумма величин - это:
- Результат операции сложения
- Итоговое значение после объединения нескольких величин
- Общая мера совокупности отдельных значений
Виды сумм величин
| Тип величины | Пример | Особенности сложения |
| Скалярные | Масса, длина | Складываются арифметически |
| Векторные | Сила, скорость | Сложение по правилу параллелограмма |
| Алгебраические | Многочлены | Сложение подобных членов |
Математические свойства суммы
Основные свойства сложения величин:
- Коммутативность: a + b = b + a
- Ассоциативность: (a + b) + c = a + (b + c)
- Существование нулевого элемента: a + 0 = a
Особые случаи:
- Сумма бесконечного ряда
- Интеграл как сумма бесконечно малых величин
- Векторная сумма
Применение в различных науках
| Область | Пример использования |
| Физика | Сумма сил, действующих на тело |
| Экономика | Суммарный доход предприятия |
| Геометрия | Сумма углов многоугольника |
| Теория вероятностей | Сумма вероятностей событий |
Графическое представление
Сумма величин может быть представлена:
- На числовой прямой
- В виде векторных диаграмм
- Как площадь под кривой
- Через геометрические фигуры
Важные замечания
При работе с суммами величин необходимо учитывать:
- Единицы измерения складываемых величин
- Природу складываемых объектов
- Допустимость операции сложения
- Пределы применимости законов сложения
Понятие суммы величин является базовым для количественного анализа в естественных и точных науках, позволяя объединять и систематизировать различные измерения и параметры.
