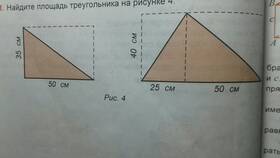
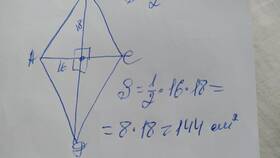Вычисление площади треугольника - одна из базовых задач геометрии, которая может решаться различными способами в зависимости от известных параметров фигуры. Рассмотрим основные методы расчета.
Содержание
Основные формулы для вычисления площади
| Метод | Формула | Когда применять |
| Через основание и высоту | S = ½ × a × h | Известны основание и высота |
| Формула Герона | S = √[p(p-a)(p-b)(p-c)] | Известны все три стороны |
| Через две стороны и угол | S = ½ × a × b × sin(α) | Известны две стороны и угол между ними |
Пошаговый расчет по формуле Герона
Вычисление полупериметра
- Сложите длины всех трех сторон треугольника: a + b + c
- Разделите полученную сумму на 2: p = (a + b + c)/2
Подстановка в формулу
- Подставьте значение полупериметра в формулу Герона
- Перемножьте значения: p × (p - a) × (p - b) × (p - c)
- Извлеките квадратный корень из полученного произведения
Пример расчета через основание и высоту
| Дано | Решение |
| Основание a = 8 см | S = ½ × 8 × 5 = 20 см² |
| Высота h = 5 см |
Особые случаи вычисления площади
- Прямоугольный треугольник:
- S = ½ × катет₁ × катет₂
- Равносторонний треугольник:
- S = (a²√3)/4
- Треугольник по координатам вершин:
- Использование формулы площади через определитель
Практические рекомендации
- Всегда проверяйте единицы измерения
- Для сложных расчетов используйте калькулятор
- При работе с координатами будьте внимательны к порядку точек
- Проверяйте возможность существования треугольника по заданным сторонам
Проверка существования треугольника
| Условие | Проверка |
| Теорема о неравенстве треугольника | a + b > c; a + c > b; b + c > a |
Правильное вычисление площади треугольника требует внимательного подхода к выбору метода расчета и точности измерений исходных параметров фигуры.